MinHash LSH Forest
MinHash LSH is useful for radius (or threshold) queries. However, top-k queries are often more useful in some cases. LSH Forest by Bawa et al. is a general LSH data structure that makes top-k query possible for many different types of LSH indexes, which include MinHash LSH. I implemented the MinHash LSH Forest, which takes a MinHash data sketch of the query set, and returns the top-k matching sets that have the approximately highest Jaccard similarities with the query set (Incorrect results of LSH Forest).
The interface of datasketch.MinHashLSHForest is similar to
datasketch.MinHashLSH,
however, it is very important to call index method after adding the
keys. Without calling the index method, the keys won’t be
searchable.
from datasketch import MinHashLSHForest, MinHash
data1 = ['minhash', 'is', 'a', 'probabilistic', 'data', 'structure', 'for',
'estimating', 'the', 'similarity', 'between', 'datasets']
data2 = ['minhash', 'is', 'a', 'probability', 'data', 'structure', 'for',
'estimating', 'the', 'similarity', 'between', 'documents']
data3 = ['minhash', 'is', 'probability', 'data', 'structure', 'for',
'estimating', 'the', 'similarity', 'between', 'documents']
# Create MinHash objects
m1 = MinHash(num_perm=128)
m2 = MinHash(num_perm=128)
m3 = MinHash(num_perm=128)
for d in data1:
m1.update(d.encode('utf8'))
for d in data2:
m2.update(d.encode('utf8'))
for d in data3:
m3.update(d.encode('utf8'))
# Create a MinHash LSH Forest with the same num_perm parameter
forest = MinHashLSHForest(num_perm=128)
# Add m2 and m3 into the index
forest.add("m2", m2)
forest.add("m3", m3)
# IMPORTANT: must call index() otherwise the keys won't be searchable
forest.index()
# Check for membership using the key
print("m2" in forest)
print("m3" in forest)
# Using m1 as the query, retrieve top 2 keys that have the higest Jaccard
result = forest.query(m1, 2)
print("Top 2 candidates", result)
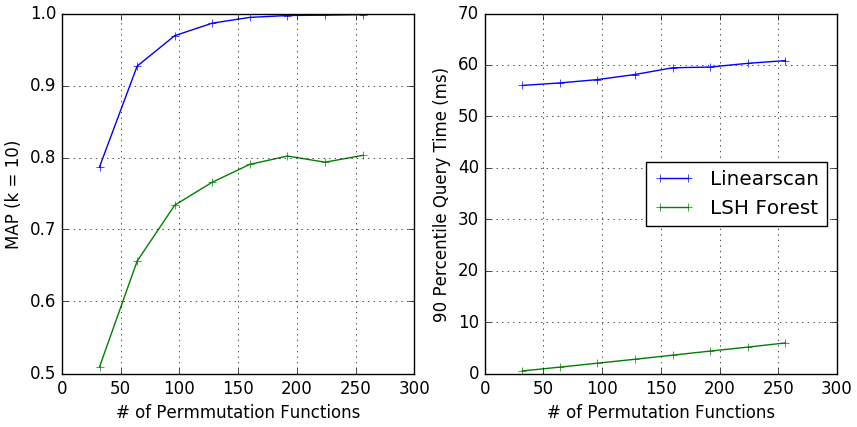
The plot below shows the mean average precision (MAP) of linear scan with MinHash and MinHash LSH Forest. Synthetic data was used. See benchmark for details.
(Optional) If you have read the LSH Forest
paper, and
understand the data structure, you may want to customize another
parameter for datasketch.MinHashLSHForest – l, the number of prefix trees
(or “LSH Trees” as in the paper) in the LSH Forest index. Different from
the paper, this implementation fixes the number of LSH functions, in
this case num_perm, and makes the maximum depth of every prefix tree
dependent on num_perm and l:
# The maximum depth of a prefix tree depends on num_perm and l
k = int(num_perm / l)
This way the interface of the datasketch.MinHashLSHForest is in coherence with
the interface of MinHash.
# There is another optional parameter l (default l=8).
forest = MinHashLSHForest(num_perm=250, l=10)
Tips for Improving Accuracy
The default parameters may not be good enough for all data. Here are some tips for improving the accuracy of LSH Forest.
Use 2*k: You can use a multiple of k (e.g., 2*k) in the argument, then compute the exact (or approximate using MinHash) Jaccard similarities of the sets referenced by the returned keys, from which you then take the top-k. For example:
# Set our k to 10.
k = 10
# Do work to create index...
# When you query, instead of use k, use 2*k.
result = forest.query(minhash, 2*k)
# Let's say you store the sets in a dictionary (not a good idea for
# millions of sets) referenced by keys, you can use them to compute
# the exact Jaccard similarities of the returned sets to your query set.
# You can also use MinHashes instead.
result = [(key, compute_jaccard(index_sets[key], query_set)
for key in result]
# Then you can take the final top-k.
result = sorted(result, key=lambda x: x[1], reverse=True)[:k]
This is often called “post-processing”. Because the total number of similarity computations is still bounded by a constant multiple of k, the performance won’t degrade too much – however you do have to keep the original sets (or MinHashes) around somewhere (in-memory, databases, etc.) so that you can make references to them.